GRR Baseline 應用


量測系統都會定期的做 GRR 測試以確保量測的可靠度。這些 GRR 測試的數據除了驗證量測系統的可靠度外，也應該收集起來建立量測系統的 baseline。建立量測系統的 baseline 可提供兩個好處：

  1. 可以藉由建立 GRR baseline 穩健的評估量測系統的能力。
  2. 每次例行性的 GRR 測試結果，都與 baseline 做比較，以分析量測能力的變化趨勢。

藉由建立 GRR baseline 穩健的評估量測系統的能力

GRR 的每次測試都會有不同的變異，所以我們很難用一次的 GRR測試結果來評斷量測系統的實際能力。為了穩健的評估量測系統的能力，我們可以收集多次 GRR 測試數據並整合成該量測系統的 baseline。

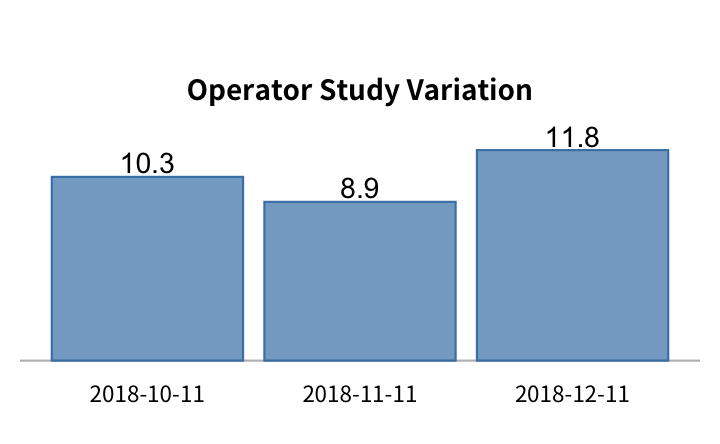
假設某一套量測系統 GRR 測試紀錄為：
Study variation \((6\sigma)\)
Variance \((\sigma^2)\)
Number of
date %GRR repeatability operator interaction part repeatability operator interaction part trial operator part
2018-10-11 14.45 8.17 10.32 0 90.13 1.85 2.96 0 225.65 3 3 9
2018-11-11 13.71 8.75 8.87 0 90.03 2.13 2.18 0 225.13 3 3 9
2018-12-11 14.47 5.87 11.80 0 90.15 0.96 3.87 0 225.74 3 3 9

我們利用 bar chart 來檢視 %GRR 跟重複性、操作員、交互作用及零件等 study variation 的走勢：



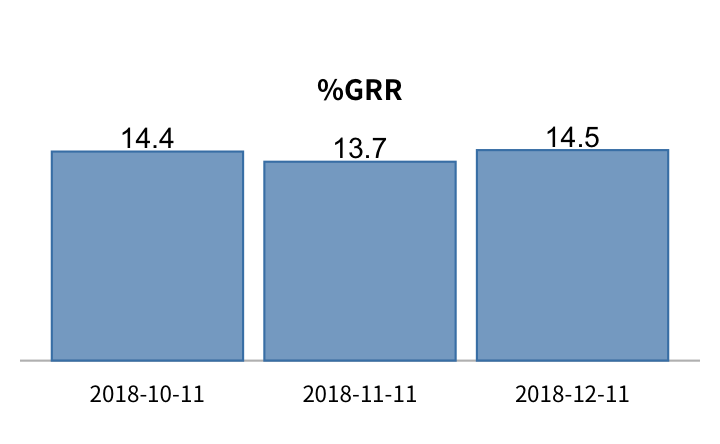
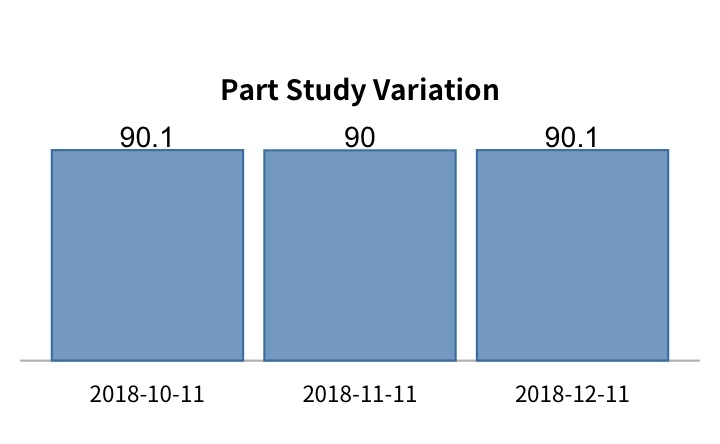
其中，零件的變異穩定的保持在 90 左右，表示在測試零件的選擇上，維持了一致的變異程度，不致於讓零件選擇的變異影響 %GRR 的計算，這一點也是在做 例行 GRR 測試時要注意的事。

操作員與零件間的交互作用持續維持在零，代表操作員並不會因不同的零件而產生不同的變異。

重複性及操作員再現性的變異則並沒有一致的結果，我們沒有理由認為最後一次或某一次的測試可以代表該量測系統的能力；比較合理的方法是將這三次的 GRR 數據整合在一起，計算出這套量測系統的 GRR baseline：

注意，由於這三次 GRR 測試的零件不一定會是相同的，所以我們不能把這三次的原始數據累積在一起，然後再套用 GRR 的計算來得到 baseline；而是要把每一次 GRR 測試的變異數跟據操作人員、零件及重複測試的自由度做加權平均來得到 baseline 的變異數，然再計算 %GRR。

Table 1: GRR Baseline
Variance Std. Dev. Study Var. % Study Var. % Contribution
Total R&R 4.651 2.157 12.940 14.2 2.0
Repeatability 1.646 1.283 7.698 8.5 0.7
Reproducibility 3.005 1.733 10.400 11.4 1.3
Operator 3.005 1.733 10.400 11.4 1.3
Operator:Part 0.000 0.000 0.000 0.0 0.0
Part 225.506 15.017 90.101 99.0 98.0
Total Variation 230.157 15.171 91.026 100.0 100.0

Baseline 中，%GRR 為 14.2, R&R 對變異數的貢獻度 (Contribution)為 2%, 其中重複性佔 0.7%、再現性佔 1.3%，沒有操作員跟零件間的交互作用。由於這個 GRR 的結果是由三次的 GRR 計算得來，會比只有一次測試的數據來的穩健，時間上也橫跨了三個月，納入了中長期的測量變異，因此比較適合用來評量量測系統的能力，及做後續 GRR 測試的比較基礎。

每次例行性的 GRR 測試結果，都與 baseline 做比較，以分析量測能力的變化。

假設第四次的 GRR 測試的結果如下：

Variance Std. Dev. Study Var. % Study Var. % Contribution
Total R&R 15.014 3.875 23.249 25.8 6.7
Repeatability 8.492 2.914 17.485 19.4 3.8
Reproducibility 6.522 2.554 15.323 17.0 2.9
Part 210.442 14.507 87.040 96.6 93.3
Total Variation 225.456 15.015 90.091 100.0 100.0


將這一次的測試數據整理併入 GRR 測試紀錄

Study variation \((6\sigma)\)
Variance \((\sigma^2)\)
Number of
date %GRR repeatability operator interaction part repeatability operator interaction part trial operator part
2018-10-11 14.45 8.17 10.32 0 90.13 1.85 2.96 0 225.65 3 3 9
2018-11-11 13.71 8.75 8.87 0 90.03 2.13 2.18 0 225.13 3 3 9
2018-12-11 14.47 5.87 11.80 0 90.15 0.96 3.87 0 225.74 3 3 9
2019-01-14 25.81 17.48 15.32 0 87.04 8.49 6.52 0 210.44 3 3 9

將 %GRR, 以及重複性、操作員、交互作用、零件的 study variation 做成 bar chart 跟 baseline (紅色橫線) 做比較：


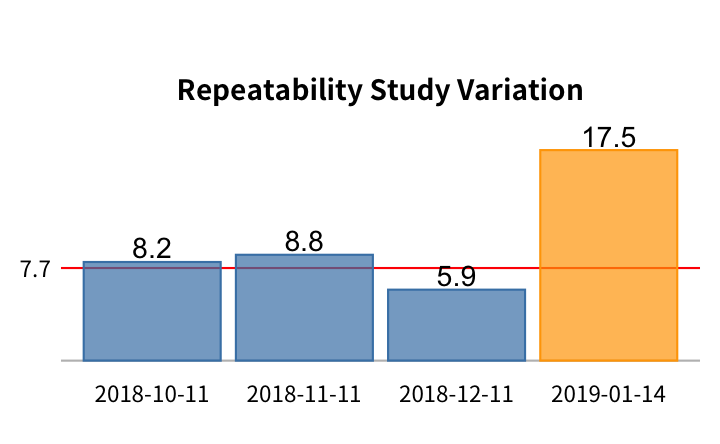
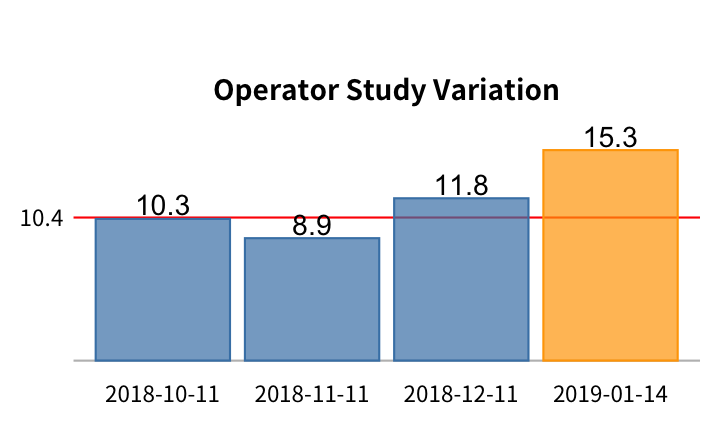
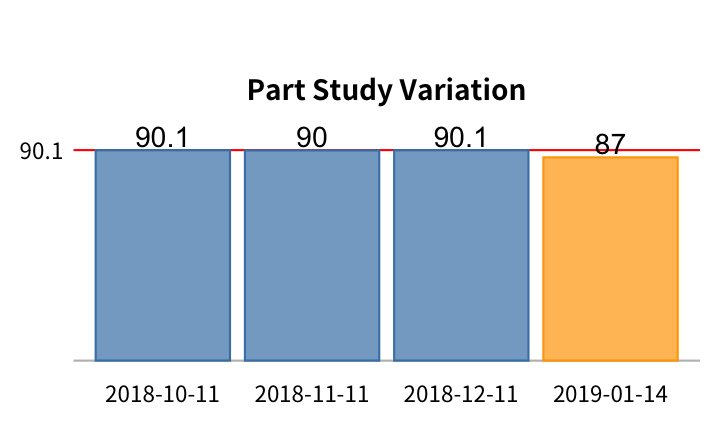
其中，2019-01-05 是最近一次 GRR 測試結果。

跟上一季的三次 GRR 比較，這次 %GRR 明顯變差。其中，重複性變差；再現性的變異也比以前稍大，但操作員與零件依舊保持沒有交互作用。源自零件的變異在這次的測試似乎沒有明顯的變化。

為了客觀的評估當次 GRR 測試結果與 baseline 的差異，我們用 F-test 比較兩者之間的變異數來決定兩者的變異是否不同。

F statistic p-value
Repeatability 5.158 0.050
Reproducibility 2.171 0.195
Part 0.933 0.508

其中， \(F\ statistic = \frac{S^2_{current\ test}}{S^2_{baseline}}\)，是當次測試的變異數除以 baseline 的變異數。


我們設定一個較不嚴格的顯著水準，α ≤ 0.1，以判斷重複性、再現性及零件的變異數在當次測試是否與 baseline 不同。在這樣的條件下：

  • 重複性被判斷為兩者不相同，最近一次測試的變異數約為 baseline 的五倍。
  • 再現性，雖然最近一次測試的變異數大約是 baseline 的二倍，但 F-test 判斷為兩者相同，因為 p-value 為 0.195，代表在這種情況下，型一錯誤(即應為相同但判斷為不同的錯誤)己接近 20%，這大於我們可接受的 10%。
  • 零件，最近一次測試的變異數接近於 baseline，F-test 也判斷兩者變異數相同。零件變異數相同是 GRR baseline 追踨及比較很重要的條件，兩次 GRR 測試的零件變異數如果不相同，是不應該來用來比較相者的 %GRR 的好壞。


從比較最近一次測試與 baseline 的結果，重複性變差應是最近一次測試 %GRR 變差的原因。我們進一步把 baseline 中包含的三次測試及當次測試的數據扣除零件及操作員再現性的變異之後，再把殘值(即以零件跟操作員為因子做 ANOVA 的 residuals)做成 X̄-R chart 以單純比較重複性的變異：


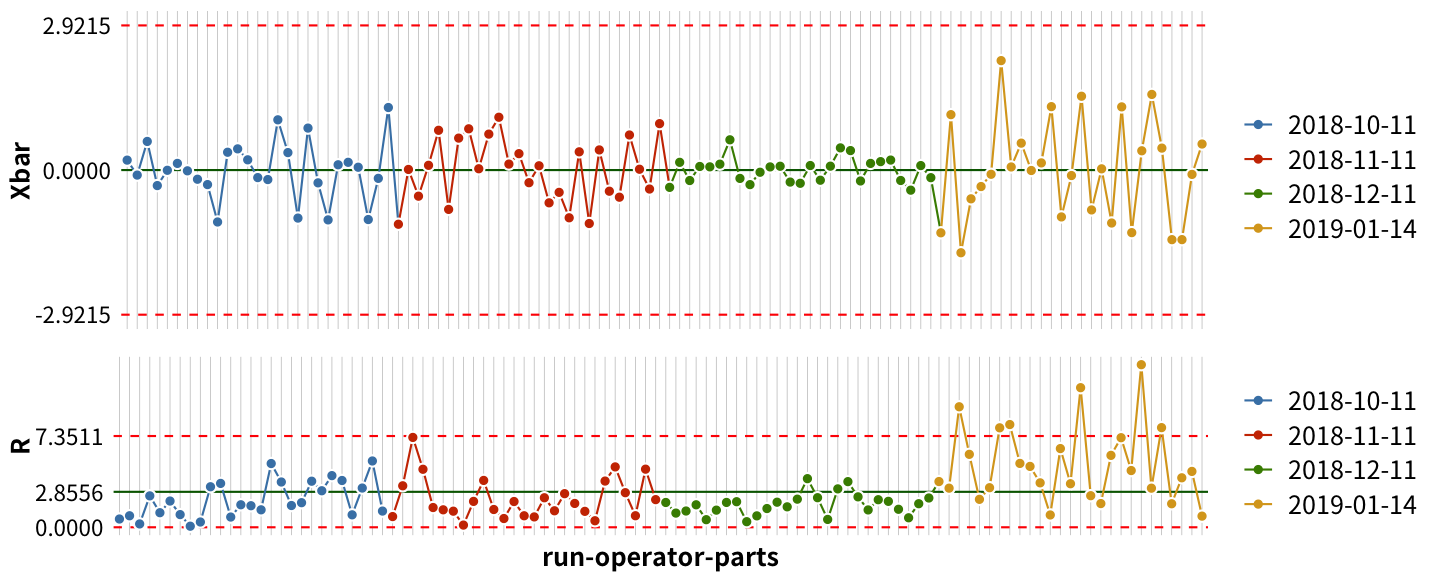
X̄-R chart 顯現出，當次量測的平均值波動及全距都比 baseline 來得大。也沒有特別的零件或操作員造成異常。

每一次的 GRR 測試除了檢視 %GRR 是否符合規範或需求之外，也應把數據收集起來，整理成該量測系統的 baseline，讓相關人員可以更穩健的評估量測系統的能力，更準確評量產品量測的不確定性，這對於生產製造或研發都會很大的助益，例如，如何處理在規格邊界的產品，或縮限產品規格時，正確的評估量測系統的能力是否足夠。當需要更進一步的改善量測系統的能力時，GRR 的歷史數據及 baseline 也能快速的提供有用的資訊及見解。