解讀 GRR 分析結果
這裡,我們模擬兩個比較極端的 GRR 例子:Good GRR 和 Bad GRR。藉由這兩個例子的結果來說明如何解讀 GRR 的分析。
GRR 基本概念
量測的變異
GRR 主要是研究量測系統的變異。我們把量測結果的變異來源分為二個類別:來自於被量測零件 (part) 的變異,以及來自於量測系統 (MS, measurement system) 本身的變異。總變異數等於零件的變異數加上量測系統的變異數:
\[\sigma^{2}_{total} = \sigma^2_{parts} + \sigma^2_{MS}\]
為了進一步評估量測系統的變異成份,我們再把量測系統的變異分為重複性(repeatability)及再現性(reproducibility)的變異,因此,總變異數可分解為三個主要的變異分量:
\[\sigma^2_{total} = \sigma^2_{parts} + \sigma^2_{repeatability} + \sigma^2_{reproducibility}\]
重複性指在相同情況下,量測系統量測相同零件,獲得相同結果的能力。再現性指量測系統在不同的情況下,例如不同的操作人員,量測系統維持量測一致性的能力。
評估量測系統重複及再現能力
量測系統的變異數加上零件的變異數,總合會為 100%。藉由分析變異數的比例,可以了解在全部的量測變異中,各個分類各佔多少比重。當需要改善量測系統能力時,這會幫助我們先釐清主要變異的來源。
標準差的單位會跟零件量測的單位相同,所以使用標準差來分析量具重複性及再現性 (簡稱為 R&R) 的結果,會產生比較有意義的比較。%GRR 是 GRR 跟 total variation 在標準差的比率(以%為單位),藉於這個比率來比較重複性跟再現性的變異與整體量測的變異,以評估量測系統的重複量測及再現性的能力。
理想上,量測的結果,來自量測系統本身的變異要越低越好。
AIAG 提供一個判斷 GRR 能力的一般準則:
- %GRR ≤ 10:量測系統的可接受。
- %GRR > 10 且 ≤ 30:量測系統可能可以接受,視製程的需求、或風險及成本來決定是否需要進一步的改善。
- %GRR > 30:量測系統不可接受。
注意:
- 不要只看
%GRR的大小來判斷量測系統是否可以接受。也要仔細檢驗在驗證 GRR 的步驟中,是否可以確實的收集到量測系統正常變異的數據。例如,挑選的零件,量測值分佈是否符合製程或產品正常範圍。當挑選的零件的分佈遠大於正常情況時,會使得%GRR變得很低,但這是過度放大零件變異的結果,並非是量測系統的正常能力。 - 重複性及再現性只是量測誤差其中的二種類別。其它量測系統的誤差還包括偏差(bias)、穏定性(stability)跟線性度(linearity),這些誤差需要運用其它的方法來研究,並不是 GRR 研究可以完成的。
GRR 分析說明
GRR table
Good GRR
| Variance | Std. Dev. | Study Var. | % Study Var. | % Contribution | % Tolerance | |
|---|---|---|---|---|---|---|
| Total R&R | 1.006 | 1.003 | 6.019 | 6.7 | 0.5 | 7.1 |
| Repeatability | 0.379 | 0.616 | 3.695 | 4.1 | 0.2 | 4.3 |
| Reproducibility | 0.627 | 0.792 | 4.752 | 5.3 | 0.3 | 5.6 |
| Part | 221.316 | 14.877 | 89.260 | 99.8 | 99.5 | 105.0 |
| Total Variation | 222.323 | 14.910 | 89.463 | 100.0 | 100.0 | 105.3 |
Bad GRR
| Variance | Std. Dev. | Study Var. | % Study Var. | % Contribution | % Tolerance | |
|---|---|---|---|---|---|---|
| Total R&R | 554.886 | 23.556 | 141.336 | 81.0 | 65.6 | 117.8 |
| Repeatability | 176.289 | 13.277 | 79.664 | 45.6 | 20.8 | 66.4 |
| Reproducibility | 378.598 | 19.458 | 116.745 | 66.9 | 44.7 | 97.3 |
| Operator | 254.948 | 15.967 | 95.803 | 54.9 | 30.1 | 79.8 |
| Operator:Part | 123.649 | 11.120 | 66.719 | 38.2 | 14.6 | 55.6 |
| Part | 291.236 | 17.066 | 102.394 | 58.7 | 34.4 | 85.3 |
| Total Variation | 846.123 | 29.088 | 174.529 | 100.0 | 100.0 | 145.4 |
GRR table 會依據 operator 跟 part 是否有交互作用有兩種不同的格式。上列的兩個表格中, Good GRR 為沒有交互作用,Bad GRR 為有交互作用。其中的差別為,有交互作用的 GRR table 會再進一步將 Reproducibility 分為 Operator 跟 Operator:Part 兩個項目,前者代表源自人員的量測變異,後者表示操作人員會對某些不同的零件有不同的量測變異。若人員操作無交互作,則表示 Reproducibility 只有含有 operator 的變異。
%GRR 一般指 %Study Var. 在 Total R&R 的值。
\[\%GRR = \frac{Total\ R\&R\ of\ StudyVar.}{Total\ variation\ of\ StudyVar.}\]
注意,%GRR 是個比率,不是比例,意義是 R&R 的變異(在此為 Study Variation, 為6倍標準差) 跟全部的變異 (total variation of study variation) 相比的結果,並不是 R&R 的變異佔全部變異的比例。
% Contribution 是每個變異分類 (component) 對於總變異的貢獻比例。計算方式是每個分類的變異數 (在 Variance 的欄位)除以 Total Variation 的變異數。
\[\%Contribution\ of\ R\&R = \frac{Variance\ of\ R\&R}{Total\ variance}\]
% Tolerance:如果有製程或產品的公差 (tolerance), 可以計算 total R&R study variation 跟 tolerance 的比率,以比較 R&R 的變異跟公差。
\[\%GRR\ of\ tolerance = \frac{Total\ R\&R\ of\ StudyVar.}{Tolerance}\]
Good GRR 的 %GRR 為 6.7,即 R&R 的變異是總變異的 6.7%。而 part 的變異是總變異的 99.8%。按照 AIAG 的準則,量測系統是可接受的。
Bad GRR 的 %GRR 為 81.0,即 R&R 的變異是總變異的 81%。而 part 的變異是總變異的 58.7%。量測系統所造成的變異遠大於零件間的變異,這樣的量測能力顯然無分辨零件的差異。
進一步分析 Bad GRR 的變異可利用 %Contribution 這個欄位的資訊。R&R 貢獻了 65.6%的變異量,其中,重複性佔了 20.8%, operator 佔了 30.1%, 而 operator 跟 part 的交互作用佔了 14.6%。雖然 operator 貢獻了最多的變異,但其餘兩種變異也不容忽略,要改善這個量測系統的能力,這三個變異來源都要同時改善。
Component of variation
Good GRR
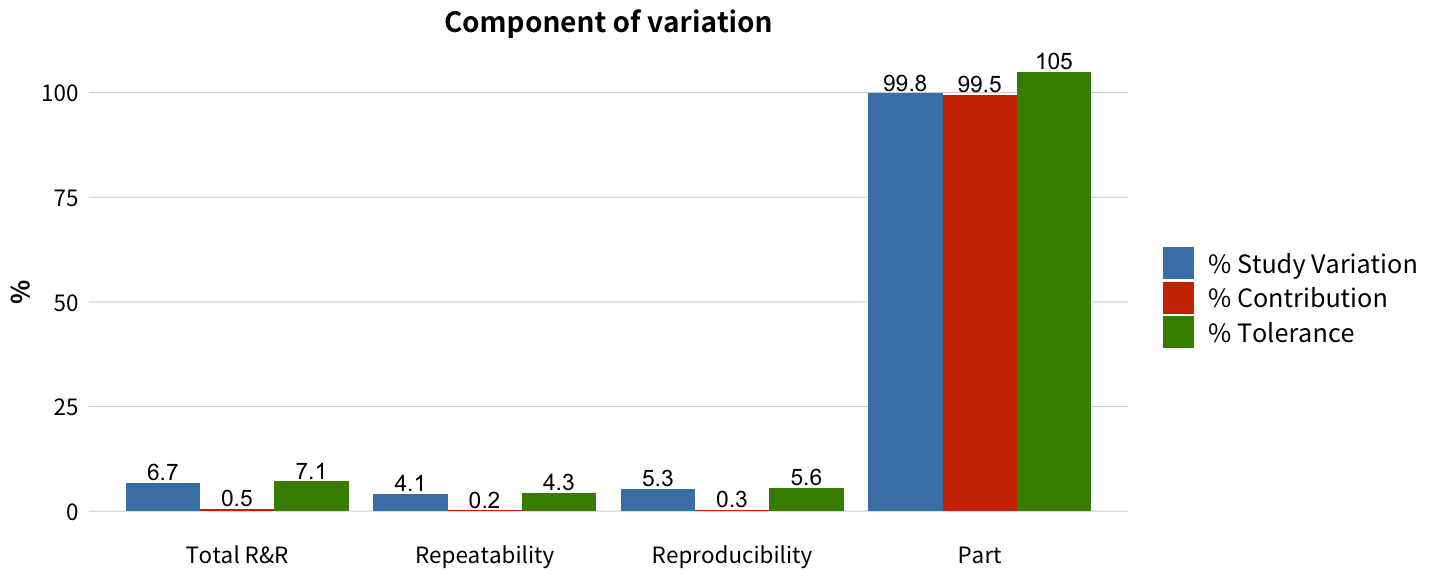
Bad GRR
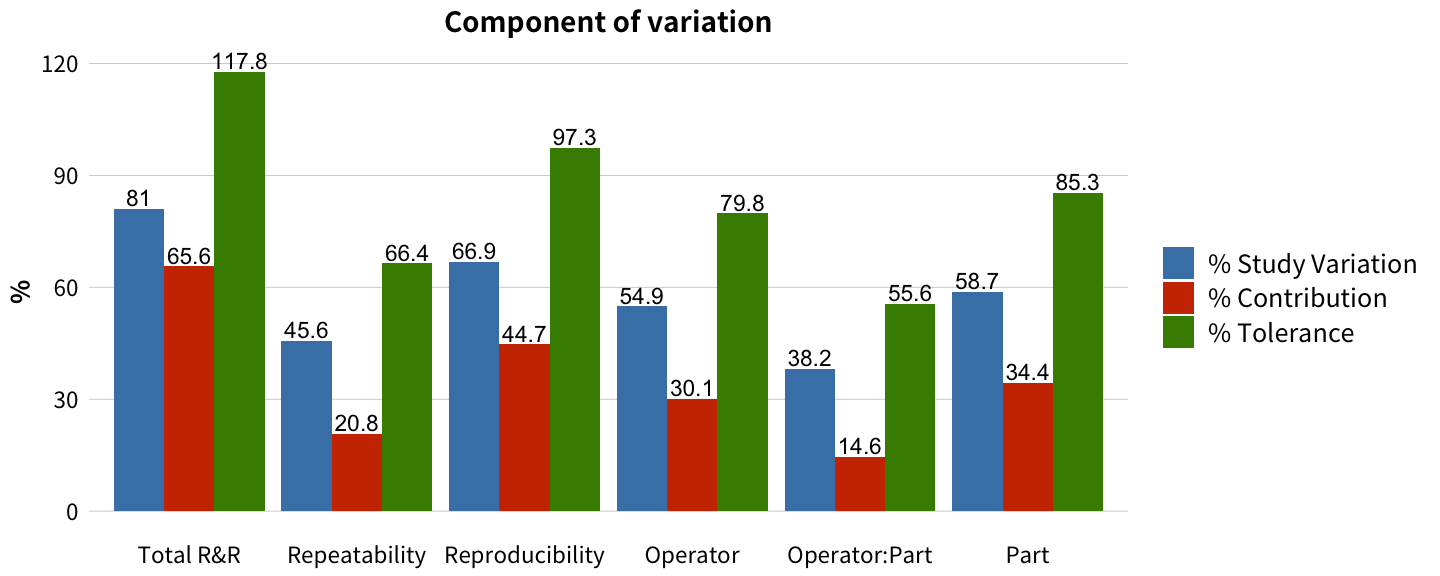
Component of variatiion 把 GRR table 中的 % Study Variation, % Contribution, 及
% Tolerance 的欄位做成長條圖來呈現變異分類的相對關係。
ANOVA table
Good GRR
| Df | Sum Sq | Mean Sq | F value | Pr(>F) | |
|---|---|---|---|---|---|
| Operator | 2 | 34.624 | 17.312 | 45.654 | 0 |
| Part | 8 | 15937.807 | 1992.226 | 5253.743 | 0 |
| Residuals | 70 | 26.544 | 0.379 |
Bad GRR
| Df | Sum Sq | Mean Sq | F value | Pr(>F) | |
|---|---|---|---|---|---|
| Operator | 2 | 14861.679 | 7430.839 | 42.152 | 0.000 |
| Part | 8 | 25346.911 | 3168.364 | 17.973 | 0.000 |
| Operator:Part | 16 | 8755.786 | 547.237 | 3.104 | 0.001 |
| Residuals | 54 | 9519.592 | 176.289 |
在做變異數分析時,會先假設 operator 跟 part 有交互作用,產出類似 Bad GRR 的 ANOVA table, 如果 Operator:Part 的 p-value 大於 0.05, 則會去除交互作用這項因子,重新再作一次變異數分析,再產生類似 Good GRR 的 ANOVA table。
在 Good GRR 中,Operator 的 p-value ,表中顯示為 Pr(>F),小於 0.05,表示 Operator 在量測時有統計上顯著的效應,意即量測結果會因 Operator 而有所不同。Operator 的效應應配合 Measuremnt by Operator 的圖來解讀。
在 Bad GRR 中,除了 Operator 有顯著的效應外,Operator 跟 Part 也出現交互作用的效應,表示 Operator 在量測零件時沒有一致性,例如量測某些零件時會偏大,而某些零件又會偏小。交互作用的效應應配合 Interaction of operator by part 圖來解讀。
X̄-R chart
Good GRR
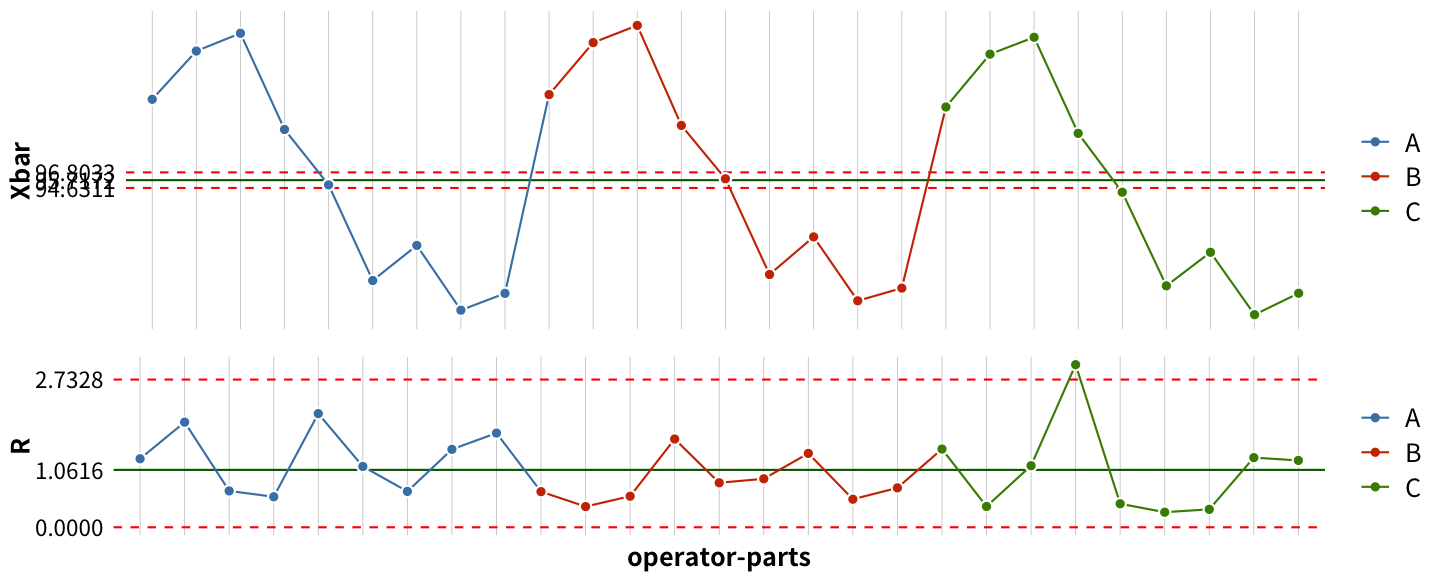
Bad GRR
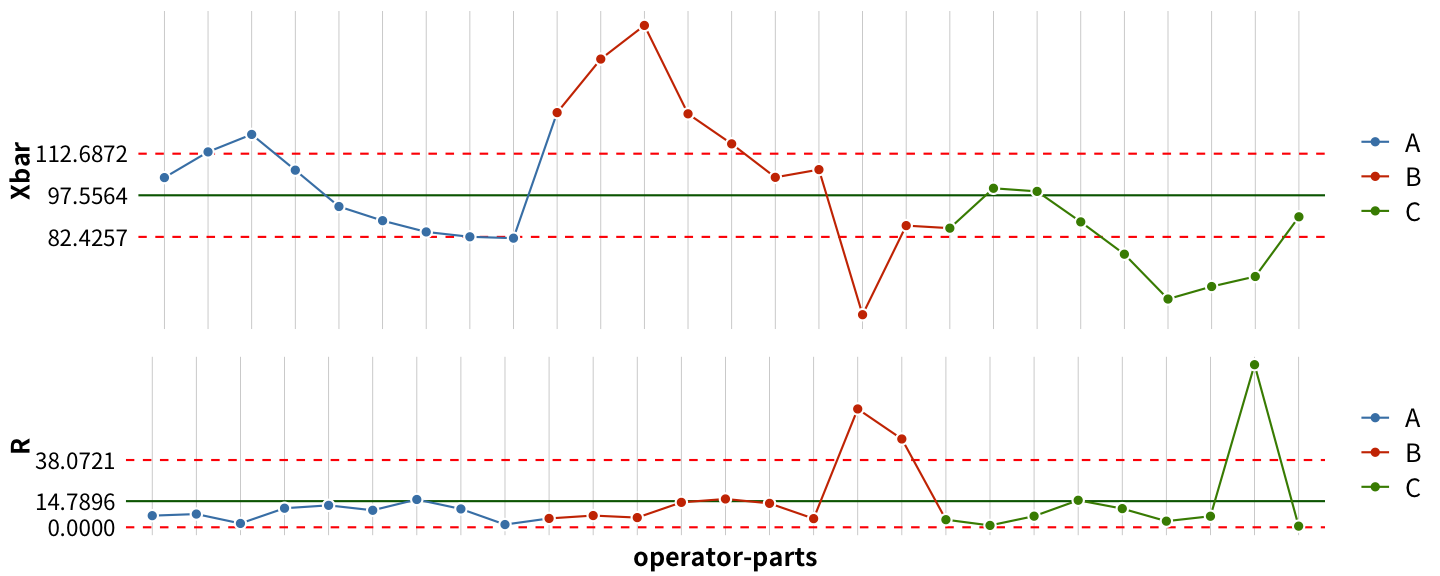
X̄ chart
- 在正常量測系統的 GRR,X̄ chart 應該呈現大部分的點都落在管制界限外。這是因為組內 的樣本數據是同一個零件重複量測的結果,所以組內的全距應該會很小,管制限界又是由組內全距計算得來,因此會得到一組間隔很小的管制界限。
- 在 Good GRR 中,有 93% 的點在管制界限外,代表量測系統可以偵測到零件間的差異。
- 在 Bad GRR 中,僅有 52% 的點在管制界限外,,代表量測系統偵測零件差異的能力有限。
R chart
- 在正常量測系統的 GRR,R chart 應該呈現所有的點都在管制界限內。R chart 在管制界限外的點代表量測的重複性不良。
- 在 Good GRR 中,有 96% 的點在管制界限內,代表量測系統有不錯的量測一致性。但其中有一點,超出管制界限。在實務上,R chart 超出管制界限的點,最好深入探究原因。
- 在 Bad GRR 中,有 89% 的點在管制界限內,這表量測系統尚有一致性。但需注意有三點超管制界限很多,而且 R chart 管制界限的上限跟平均值相比,也顯得太大,這些顯示即使大部分的點都在管制內,但量測的重複性可能是有問題的。比對 GRR table, Repeatability 的 標準差是 13.2, 而 Part 的標準差是 17.06, 相差並不大,顯示量測系統的重複性在量測每一個零件時,雖有一致性,但是是一致性的不好。
Measuremnt by Operator
Good GRR
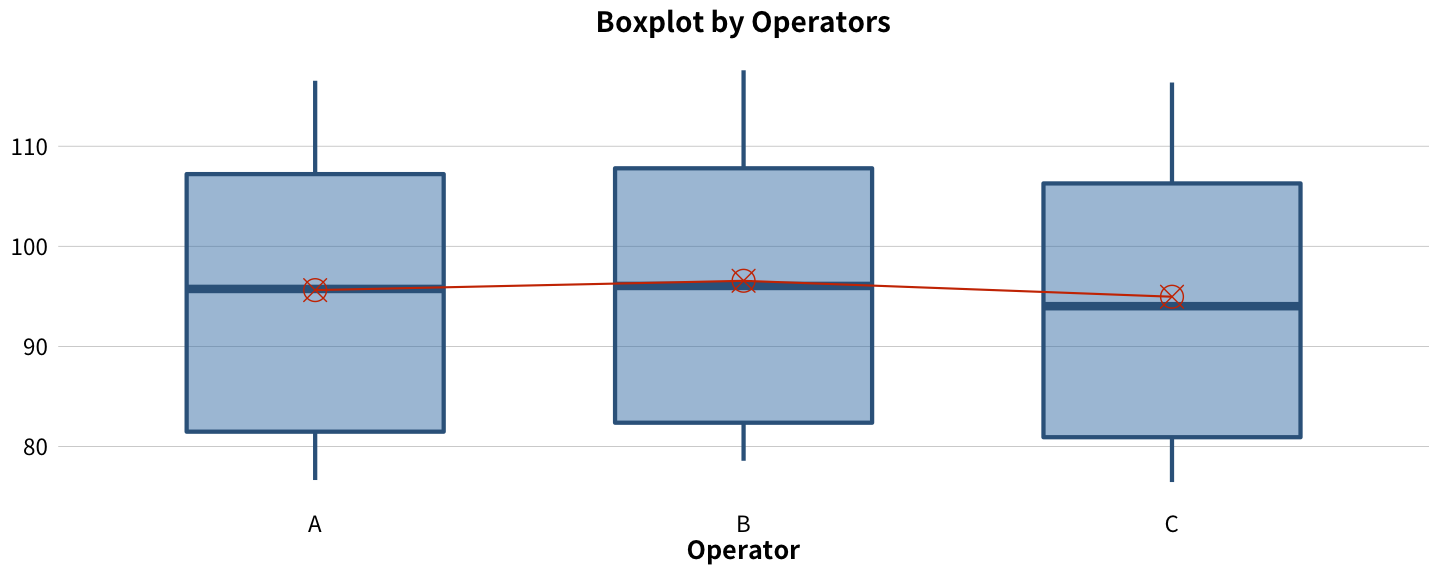
Bad GRR
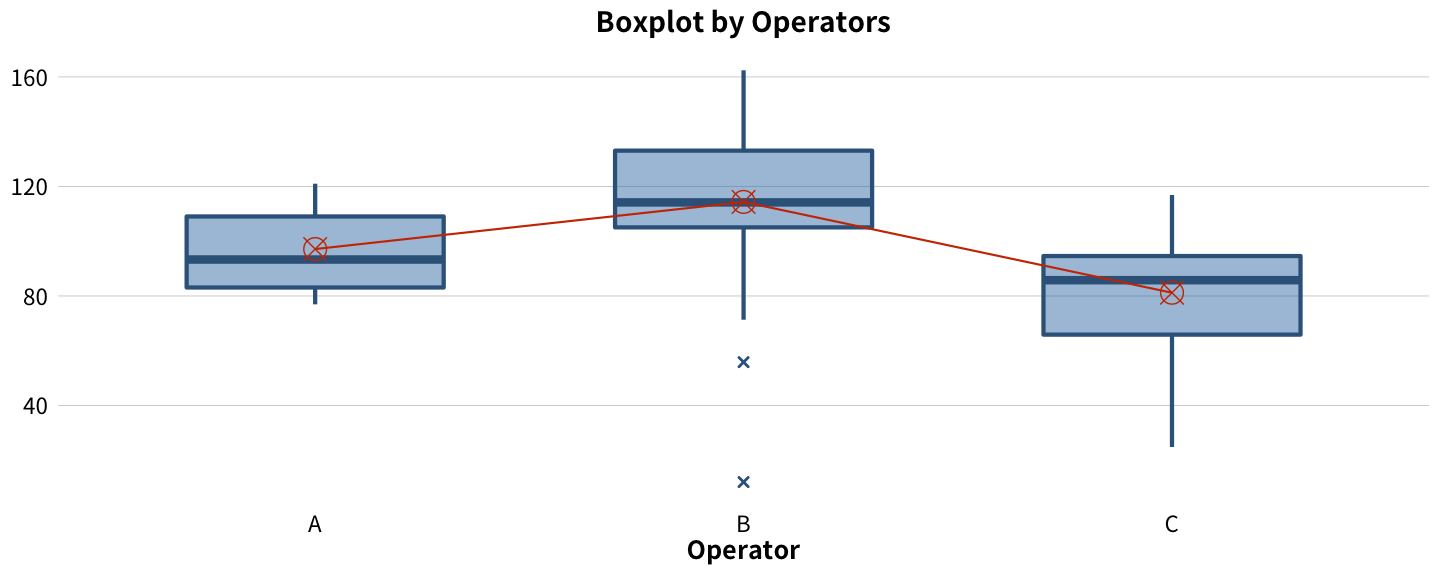
- 配合 ANOVA p-value,不論 Good GRR 或 Bad GRR,Operator 都有統計上顯著的效應,表示三個操作人員的量測有不一致的結果。Bad GRR 的盒鬚圖很明確的顯示跟 A 相比,B 量測偏高,而 C 偏低。Good GRR 也有這個趨勢,但不像 Bad GRR 那麼明顯。
- 比較三個 Operator 的盒鬚圖長度和離群值的分佈,可以分析三個 Operator 在量測時是否產生相同的變異。在 Bad GRR 中,Operator B 跟 C 有比 A 更廣的分佈,表示 B 跟 C 在量測時有較大的變異。在 GRR 分析的應用程式中,會運用 Levene’s test 做變異數的比較以輔助判斷 Operator 之間是否有不同的量測變異。
Interaction of operator by part
Good GRR

Bad GRR

Good GRR 的 ANOVA p-value 判斷 Operator 跟 Part 沒有交互作用。 觀察交互作用圖,三條折線保持一致的趨勢,同樣這也表示 Operator 跟 Part 沒有交互作用。
而在 Bad GRR,ANOVA 判斷 Operator 跟 Part 有交互作用。在圖中,三條折線有互相交叉的現象,其中 Operator B 在量測第一到第七個 part 時都顯得偏高,但在量測第八個時反而偏低,第九個 part 時就沒有這個現象,顯示 Operator B 在量測 part 時,其偏差會因 part 而不同,表示 Operator 跟 Part 有交互作用。
Measurement by parts
Good GRR
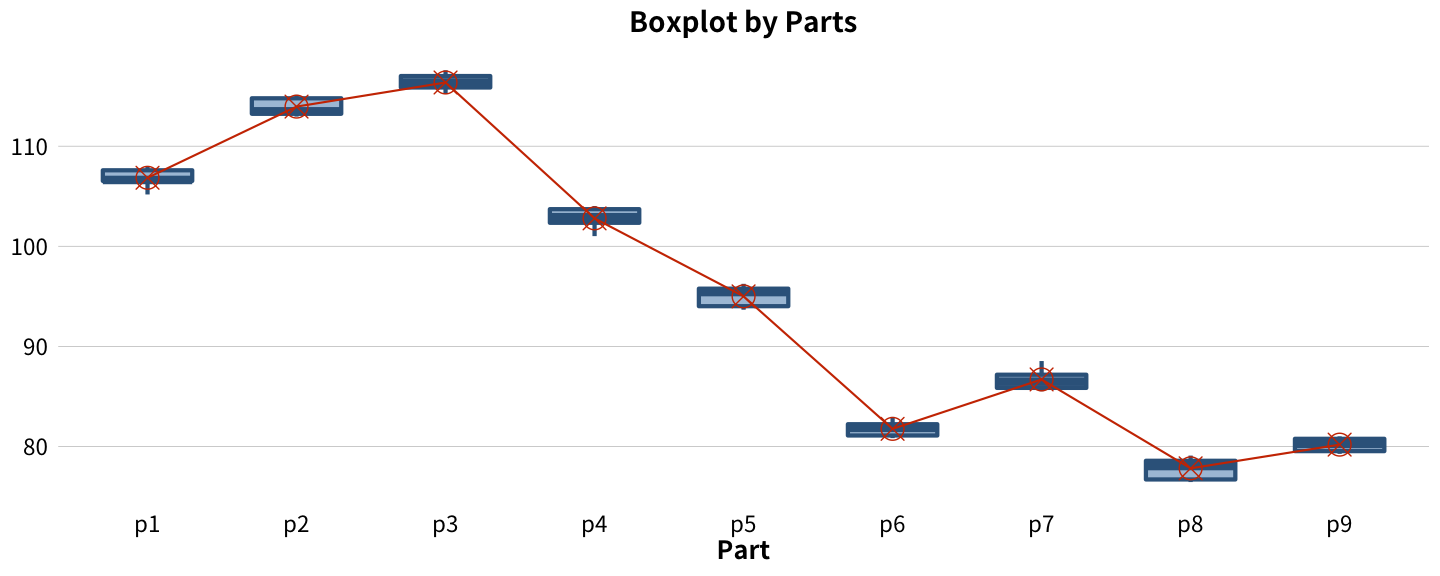
Bad GRR

- Good GRR 可以明顯的區別出 part 間的差異,但在 Bad GRR,part 間的區別就不明顯。
- 比較盒鬚圖的長度及離群值的分佈,可以分析每個零件被量測時,是否帶有相同的變異。在 GRR 分析的應用程式中,會運用 Levene’s test 做變異數的比較以輔助判斷。