製造瘋AI前，先瞭解應用模型的風險及效能評估

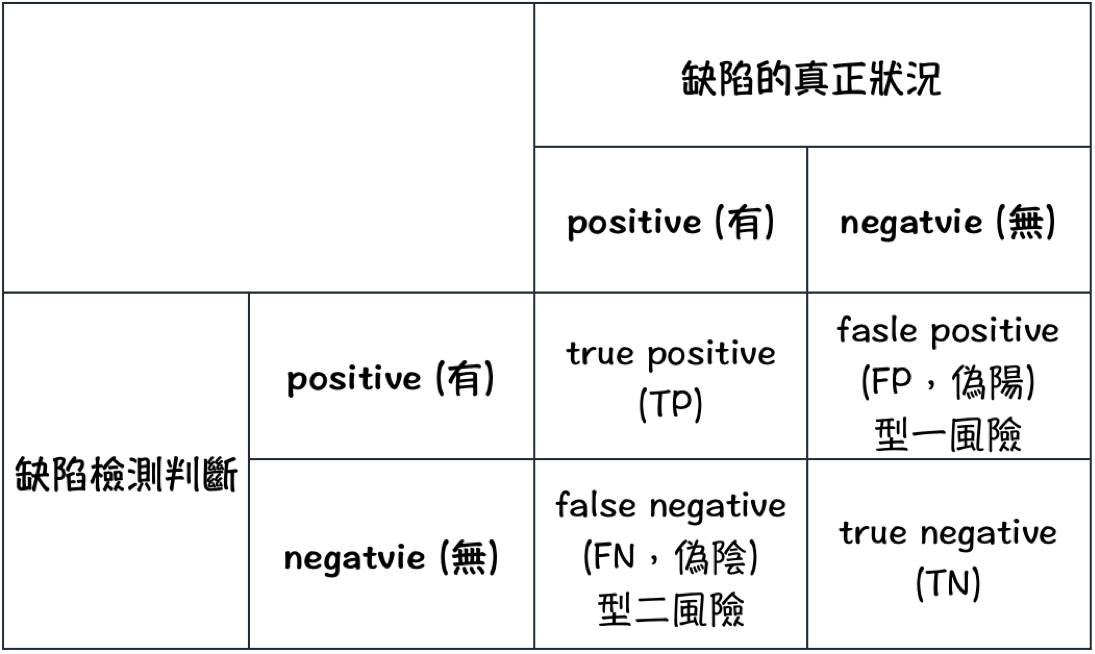
預測判斷的風險：型一及型二風險

當應用模型做出判斷後，判斷錯誤的風險有二種：

• 型一風險：當產品無缺陷，卻被判定為有缺陷。我們會把好的貨品報廢掉或重工，形成浪費。這類型的判斷錯誤稱之為型一錯誤。
• 型二風險：當產品有缺陷，卻被判定為無缺陷。我們會把壞的貨品送到下游或到客戶手上，前者造成流程上的浪費，後者除退貨的成本損失外，有可能是商譽及商機的損失，甚至造成生命的危害。這類型的判斷錯誤稱之為型二錯誤。

由 confusion matrix 可發展出數個指標來評估模型的效益及風險。我們可以從兩個面向來了解這些指標。一個是從模型歸類的能力來看，另外則是從模型預測判斷結果的信心度來看。

從正確歸類的能力來看模型評估指標

也就是模型是否能正確的判斷出產品是否有缺陷，相關的指標有：

• TPR (true positive rate，真陽性率) ＝ \(\frac {TP}{TP+FN}\)，又稱敏感度、召回率或檢定力: 如果真值為 positive，檢測結果也為 positive 的機率。也就是能正確判斷出有缺陷的機率。
• TNR (true negative rate，真陰性率) ＝ \(\frac {TN}{TN+FP}\)，也稱為特異度: 如果真值為negative，檢測結果也為 negative 的機率。即能正確判斷出無缺陷的機率。
• FPR (false positive rate，偽陽性率) = 1-TNR，也稱為 fall-out，即型一錯誤的機率；把好的產品誤殺的機率。
• FNR (false negative rate，偽陰性率) = 1-TPR，也稱為 miss-rate，即型二錯誤的機率；把壞的產品誤放的機率。
• 準確度 (Accuracy) = \(\frac {TP+TN}{TP+TN+FP+FN}\)，正確判斷出產品有無缺陷的能力。

乍看之下，準確度是一個評估模型的好指標，但是要注意，當建立模型的類別數目不均衡時，準確度就會有嚴重失準的問題。例如，假設我們建立的模型的數據中有97個樣本是無缺陷，而只有3個樣本是有缺陷，那麼模型會頃向把所有的檢測物件都判斷為無缺陷，因為這樣就有 97% 的高準確率，但事實上這個模型卻無偵測出缺陷的能力。所以，以準確度評量模型時，不能只是看準確度的數字，也要同時注意樣本數的均勻度。

從檢測結果的信心度來看模型評估指標

也就是當判斷結果已經出來時，我們對這個結果會有多少信心？相關的指標有：

• PPV (positive predictive value) = \(\frac {TP}{TP+FP}\)，也稱為精確度：如果判斷的結果為 positive，真值為 positive 的可能性。即判斷為有缺陷，而這個判是正確的可能性。
• NPV (negative predictive value) ＝ \(\frac {TN}{TN+FN}\)：判斷結果為 negative，其真值為 negative 的可能性。即檢測判斷為無缺陷，而這個判是正確的可能性。
• FDR (false discovery rate) = 1 - PPV：若判斷為有缺陷，這個判斷是錯誤的可能性。
• FOR (false omission rate) = 1 - NPV：若判斷為無缺陷，這個判斷是錯誤的可能性。

PPV 及 NPV 越高代表對判斷結果的信心度越高，而越高的 FDR 及 FOR 表示判斷錯誤的可能性越大。

舉例來說，假設某一個缺陷檢查站，不論用人工或機器或者再加上AI，如果檢測模型的 FOR 為 5%，而某一批產品良率為 90%，則其中有 4.5% 通過檢驗的產品有可能是有缺陷的但被誤放。若 FDR 也是 5%，則 10% 的良率損失中，只有 0.5% 損失可能是誤殺，即沒有缺陷但被判定為有缺陷。在高良率時，FOR 會 比 FDR 來的影響程度更大。當然在實務上，不是每一種缺陷都會有相同的代價，意思是統包成良率之後再來評估 FDR 跟 FOR 的影響，會失去真正的意義，而應是依缺陷影響的權重來評量。

平衡型一和型二錯誤的指標

我們可以透過改善檢測方式及分類演算法來提升判斷準確度，來同時降低型一跟型二的錯誤率，一但檢測的工具方法及分類演算法確定之後，降低某一種型態的錯誤率就會增加另一種型態的錯誤率。所以在建立預測判斷模型時需要有同時平衡這兩種類型的錯誤率，ROC-AUC 為其中最常使用的一種方法。

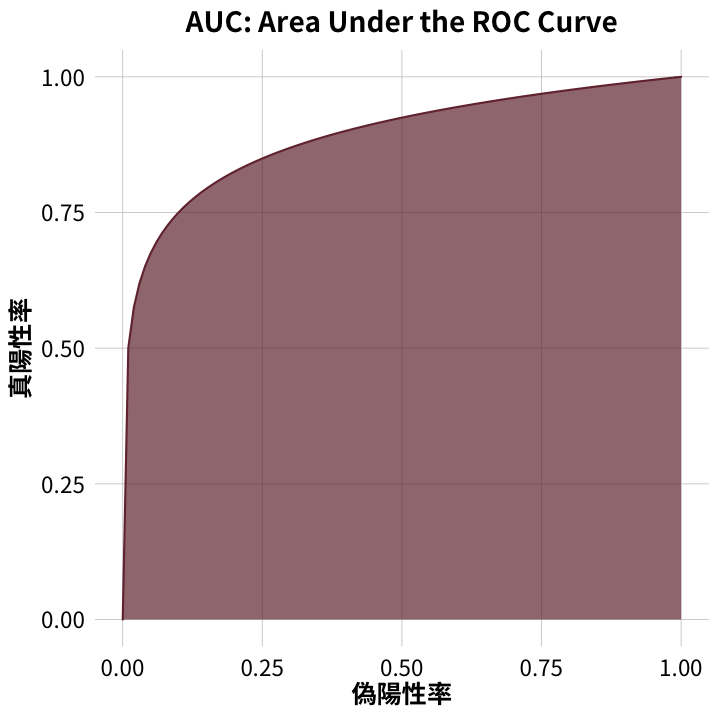
ROC (receiver operating characteristic) curve 由真陽性率 (TPR，true positive rate，敏感度或召回率) 跟偽陽性率 (FPR，false positive rate ) 兩個指標組成的曲線圖。典型的 ROC curve 如圖一，而完美不產生錯誤判斷的模型的 ROC curve 如圖二，沒有效能的模型的 ROC curve 如圖三。效能愈好的模型其 ROC curve 會愈接近圖二，愈差則愈接近圖三。

除非是不會產生判斷錯誤的完美模型，否則提高了真陽性率就會以某種程度增加偽陽性率，也就是降低型二錯誤率會增加型一錯誤率，反之亦然。ROC 提供一個視覺化的工具，讓我們可以找到平衡真陽性率跟偽陽性率之間的最佳決策點。

AUC 是指在 ROC curve 之下的面積比例，完美模型的 AUC 為 100%，無效模型的 AUC 為 50%。其餘會在 50% 跟 100% 之間，愈接近 100% 是愈好的模型。由於分類演算法會影響模型的效能，在評估不同演算法的模型效能時，AUC 是一個實用的指標。

型一跟型二風險之間的得失權衡必須依照模型應用的情境來做選擇，例如產品經過檢測後就會到客戶手上，跟還會經過一下站的工序及檢測的損失成本就不同。或者當產品的缺陷會造成致命性的危害時，這個時候犯型二誤差的代價就遠比犯型一誤差來的大很多，在這種狀況下，敏感度就遠比精確度來的重要。

決策者要理性的計算型一及型二風險的成本，做出最佳的選擇。透過理解及運用這些指標，決策者及使用者可以更有深度的了解模型的能力及誤判的風險，讓模型能發揮應有的功能而不致於過度相信模型的預測或判斷能力反而低估風險，或者根本忽略了應用模型的風險評估及管制措施，反而造成更大的損失。